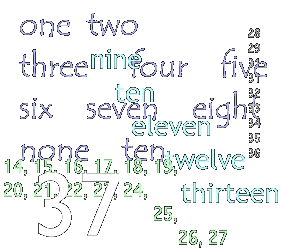Intermission brain challenge!

on
For the last few days I've had houseguests in town visiting* - hence the lack of attention I've been paying to blogging. But I bundled them back into the car for the trip back to Iowa this afternoon, so in light of the fact that i was a little light today, I present...the brain scrambler!!!!

Pretty neat huh? I have to admit it took me a while to figure out how it works. Can *you* figure it out? I'll post the answer during lunch tomorrow in the comments. Yay fun!

* For example, apparently they saw a guy get hit by a CTA bus this afternoon on Michigan Ave, but I'll get to that story tomorrow, it's late and I'm sleepy.

Comments

Ted Pavlic said…
On a similar note, the documentary _Wordplay_ about the Times crossword puzzle and the Stamford annual crossword competition was REALLY fun. Very entertaining. Very funny.

See it.
July 18, 2006 11:54 PM
Ted Pavlic said…
(but but but... it says it's not a dumb math teaser... but it IS a dumb math teaser! Base-N numbers will always lead to multiples of (N-1)! (try doing it in another base) It's like high school number theory. Am I a pedantic jacka$$ know-it-all for being upset by this?)
July 19, 2006 12:05 AM
grrrbear said…
Yes, it is mostly just another dumb bath teaser. But that's not what makes this one so elegantly beautiful. The great thing is how they randomized symbol for all the multiples of 9 each time you choose. So every time you do it, you get a different symbol, which helps reinforce the believe that it truly is random ("I get a different symbol each time, so it *can't* just be a math trick!").

But I didn't know that this worked for other bases. I just noticed that all the multiples of 9 always matched the symbol that came up. Thanks for the math lesson Theo!
July 19, 2006 1:17 PM
Ted Pavlic said…
Quick explanation...

You're always subtracting off the 1's column, so it doesn't matter. 34 - 4 = 30. 45 - 5 = 40.

So what you're really doing is subtracting the N's (where N is your base) column from a number that is a multiple of the base (in other words, a number that ends in 0).

In fact, you'll always end up with:

n*N - n

where "n" is the N's column and N is the base. Factor it out...

n*(N-1)

And there you have it... The result is always a multiple of N-1.

Bada-bing. The key was in subtracting off the 1's column to get a number that ends in 0. Woot.
July 19, 2006 1:44 PM
Post a Comment